| 7.角度背景の現実 |
さあ、ゲームも7回終盤に差し掛かった所で
やけにタイトルが重々しい感じだが
しつこいかな現実的に、実用的に考えて行きたいと思う。
この背景を角度から求めるやり方を紹介している背景レポート
実にもう第七回目だがここにきて重大な落とし穴があるのだ。
うん・・・それはどういう事かというと
どんな絵や写真を見ても
「これは〜°視界角の絵です、良かったら見て下さい」とか
「これは〜°の視界のものです、ご参考にどうぞ」とか
「これは〜°の絵です、素晴らしいですね〜°って」とか
「これは〜°の世界ですのよ」とか
これは・・・
ギャアアアアアア!!!!
無いのだ。
どこにも視界の角度なんかを馬鹿丁寧に書いてある絵や写真なんて無いのだ
悲しいかな角度背景・・・
ましてや真っ白なキャンバスから世界を描いて行く絵描きさんなら
まず基本となる地面パースを描いて・・・
そこに合うようにモノを描いて・・・なんて事はしない。
地平線を描いて、それを基準にモノをフィーリングで描いたり
パパっと家並みを描いてそれにパースを合わせて描いたりと
とにかくパースよりもモノの大きさ、構図などが一番重要で
もちろんパースから描く人もいるだろうが、多くの絵描きさんにとっては
実際パースなんてものは修正の付け焼刃程度に使っているような気がする。
そう、これが角度背景の現実なんだ
しかしだ、もう7回目だよこのレポート・・・w
どうするよって
今までの苦労を無駄にはしないさ〜!
前置きが長くなったが、これこそがレポート根性!
「講座」っぽいけど「レポート」だと言い張る理由!
ちゃちゃっと「絵から角度を求めるやり方」
そろそろご紹介いたします・・・。
|
そうだな・・・たとえば
2mの変なオブジェが8m先にあったとする。
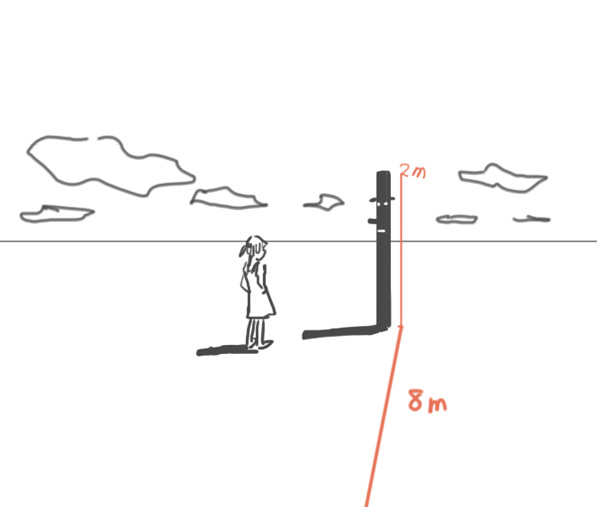
こんな感じか・・・
(画像反転で視野確認。)
この後、他にモノを描き加えたいのだが
少し不安なので地面パースを描くとするとしようか
と、まあこのへんてこな絵なのだが
すでにこの絵の角度が求められる状況なのだ。
そう、それに必要なのは
対象とするモノとの距離とそのモノの本来の大きさ
これだけでいい。
道路の幅だとか、電信柱からの距離、家の高さ、家までの距離などなど
日常生活の中にもある程度決められた大きさ、長さを持つものは非常に多い
そういったものを描く上では、それらを活用すると非常に楽になるだろう。
ところで今回のこの絵は
モノとの距離がだいたい8m、そのモノの高さを2mだとする。
そこで、いろいろ説明するのもアリなのだが
「公式暗記」のような感じで以下の式を参考にして欲しい
(どうしてそういう式になるのかは必要な人だけ見てくれ)
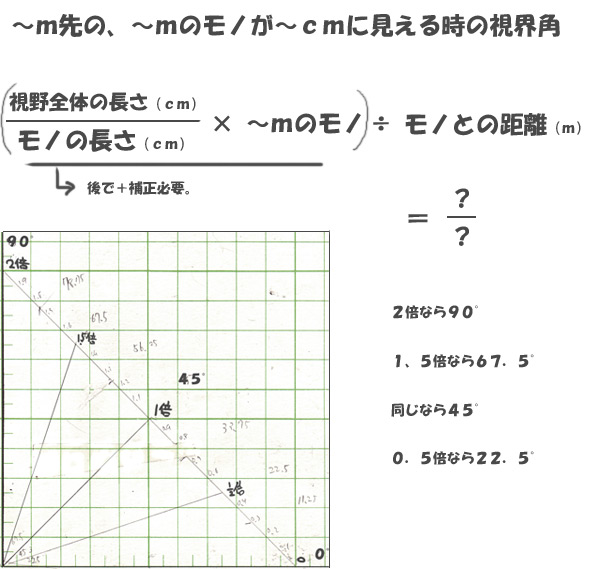
なんかいろいろ出てきたが
とりあえずこの上の式に代入すれば変な数字が出る。それ次第で角度が決まるというものだ。
よし、じゃあ。お疲れモード全開でやっていこうか・・・笑
おおまかに言えば、画面の大きさに対してその対象物がどのくらいの割合なら視野は何°かというもので
この式のカッコの中のものは
つまるところ、このオブジェ(対象となるモノ)が画面いっぱいに伸びたら何mになるのかという式だ。
もちろん定規を使って絵を測るわけだが
絵に対してそのモノが小さい場合は特に補正が必要だ
理由は簡単で、このオブジェを一個上に追加したとしよう。
定規は地面と接しているオブジェの長さを測っているから
定規で測った長さを倍にしても遠近感で
実際は追加したオブジェは2mちょいなくてはならない事になるからだ。
そういう時は最後に求められる角度に若干+αを加えた角度にして欲しい
※なるべく大きいものを対象物に選ぼう。
(絵に対してどのくらいの割合の対象物であれば、どのくらいの補正が必要かは
後々時間をみてレポート提出できたらいいなと思っている)
まあとりあえずやってみよう。
定規で測ったところ、オブジェは4、5cm。キャンバスの高さは15cmあった。
これで最初は15÷4,5で3,3333。
それに対象物となる本来のモノが2mだから、3,333をかけて
6.66666となる。
それで最後に距離の8mで割る。
答え0.83
と出ただろうか。
そして画像左下で0.83を探す
だいたい40°〜と言ったところだろうか
これに気分で補正をかけて45°としよう笑
つまりこの絵は45°視界の絵ということになる。
では次回は今までやってきたことをこれに応用して1m地面パースを描いてみることにする。
|
|