| 10.続・超実践編 |

パース等は使わずフィーリングでこんな絵を描いてみた。
ここから1m幅の道を描こうと思う。
自分も背景レポを見ながらの作業だったので
よければ別窓で「背景レポート7:角度背景の現実」をご覧いただければと思う。
7の下の方によくわからないような数式が載ってある
その式に必要なものの長さを求めてみる。
1、青色 「キャンバスの縦の長さ(cm)」
2、赤色 「比較対照とするモノの見える長さ(cm)」
3、緑色 「比較対照とするモノの実際の長さ(m)」
4、橙色 「比較対照からの実際の距離(m)」
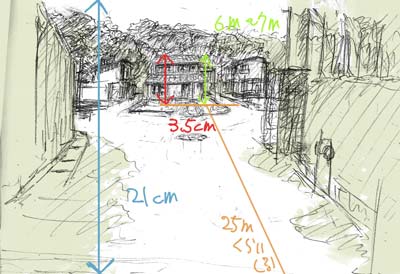
とりあえず家からの距離をだいたい25mとしよう。
(間違っていても後から修正出来る。)
キャンバスの長さは21cm。家はだいたい6〜7mだとして、実際は3、5cmだった。
さて、これらを式に代入してこの絵の縦の角度(視界角度)を求める。
{(キャンバスの長さ21cm ÷ 家の長さ3.5cm) ×6mの家} ÷家との距離25m
=36÷25=1.44
ということは 下の図で見るところ だいたい“65度”ということにしよう。
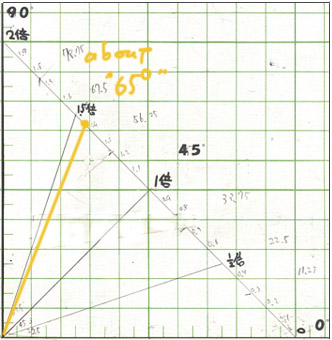
つまり現段階で仮にこの絵は縦視界「65°の絵」ということだ
この65°というのを縦全部の縦メモリとして、今度は消失点から足下までの視野角度を求める
だいたい42°としよう。最初求める時は結構数値が間違っていたりするので
後から直すことを前提にこのあたりはちゃちゃっと進んでいく事にする。
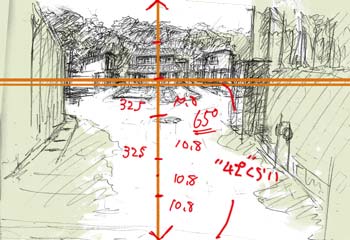
絵の角度を求め終わり縦メモリを付け加えたので
今度は視野の高さを求める
よし。だいたい、1、2mとしよう。
視点の高さ1、2mの時の角度を調べると・・・
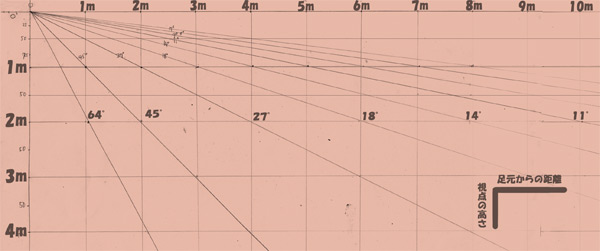
(↓視点の高さ →距離)
1m先で50度、2mなら30度
3mの時に約20度くらいを通る。
4mなら16度、5mなら14度弱・・・と
ではそれぞれを縦メモリに描き加えていこう。
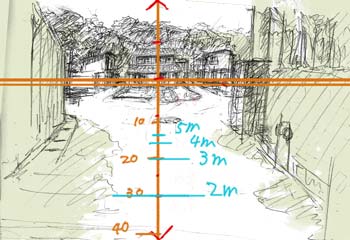
こんな感じになっただろうか。
もちろんこのまま横メモリを書き加え1m地面パースを描くのも有りだが・・・
特に2m先、3m先あたりを見て欲しい。
ちょっと変じゃないだろうか
いくら1、2mの視点の高さとは言え、2m先はそんなに遠く感じるものだろうかと
そうだ、ここからが本番だ!笑(ぇ
フィーリングでいいので2m先は何度くらいのところに来るのかというのをイメージする。
ベッドだとか、畳の縦の長さ+αくらいの長さだ。
そう考えれば35度〜40度くらいのところにあると踏んだ
つまりイメージで言うならこういうことになる↓
(↑の絵と比較して欲しい
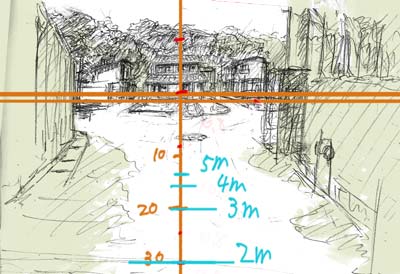
5mあたりを見ても、これならさっきよりも納得だろう。
それならこの絵の下視界角は32°くらい。縦全体なら50°くらいだろうか
そしてここが一番大切なところでもあるが
そこから最初、式で代入した何が間違っていたのかという事を考える。
しばし回想
{(キャンバスの長さ21cm ÷ 家の長さ3.5cm) ×6mの家} ÷家との距離25m
=36÷25=1.44

・・・うーむ。
当初65°という答えが求められたが・・・実際、50度ってことは1、1倍くらい。 なら
{(キャンバスの長さ21cm ÷ 家の長さ3.5cm) ×6mの家} ÷家との距離25m=「1.1」 :「1」
でなくてはならない。
左の式を家(モノ)との距離で割った時に1,44倍というのだから
左の式が大きすぎるのか、右の式 家との距離が短すぎるのかのどちからということになる
左の式の場合、定規で測ったキャンバスや家の長さは確固たるものだろう
変だとすれば家の長さだが、6mというのはかなり標準サイズだ・・・
ならば間違っていたのは家との距離ということだ!
でははやる気持ちを抑えつつさっそく逆算していこう。
{(キャンバスの長さ21cm ÷ 家の長さ3.5cm) ×6mの家} ÷家との距離「?」=1,1
36÷?=1,1 家との距離=32,7m!
「ああー。そう言われてみれば25mは少し短かったですびゃ♪」・・・バキバキボコ!! ズピューン
ぎゃああぁぁぁ・・・
かくしてこの絵に平和は訪れた
と。いやあ結構、使えるものだなこの背景レポート・・・w
全く使っていなかったので、何気に自分が一番びっくりした笑
こういう風にやっていけば、モノを見る目というのが自然と培われていくだろう
失敗を恐れずにどんどんやっていって、変だと思ったら直していってくれればと思うし
分からない部分があれば気軽にpixivとかのメッセージなり掲示板なり言っていただければ
綺麗なお姉ちゃんが貴殿のご自宅で懇切丁寧に(ry
私めでよろしければ、該当部分を説明したメッセージをお送り致します・・・(w
さてさて、これで絵の角度と消失点から下の角度も分かった。
あとはここから横メモリを書き加え、1m地面パースを作ってみようじゃないか!
|
|