| 2.角度と視点の高さ |
前のところでは70°での視野の話をしたが
今回は70°とかの前に、少し昔をおさらいしてみながら進めていこうと思う
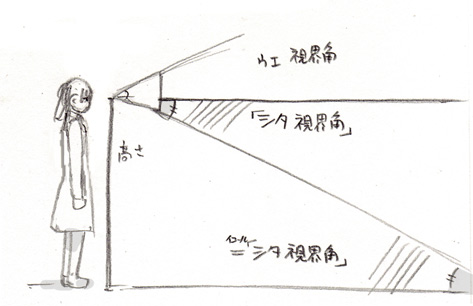
このメガホンから伸びるウエ視界角と「シタ視界角」という意味はわかるだろうか。
ウエ視界角は前回の25°、「シタ視界角」は45°というアレだ
ちょっと数学チックな話になる。
この「シタ視界角」と下にある (イコール)=「シタ視界角」。
二つ足せばちょうど長方形の形になることはご存知だろうか
だな・・・。
うん、知っているはずだ。
長方形を斜めに線を入れたものと一緒だ
そして対称となる角度も一緒だという事もご存知だろう。
そう、角度と高ささえ分かれば距離が出るというアレを今回やる
しかしそんな事は随分昔の話である以上
どんなやつだったか少し思い出しながら練習してみるとしよう。
(※説明などいらん!時間が無いぞ、こんちくしょー!
という人は下に派手な表があるのでそこまで飛んでくれ)
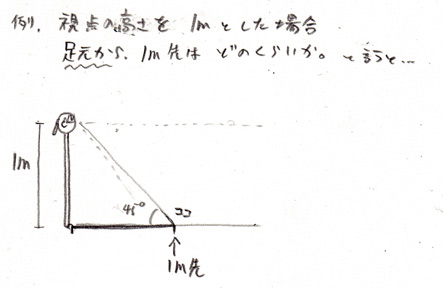
読めるか・・・。古代文字を解読するように貴重な集中力をここで使わせてしまって申し訳ない
この絵の説明をすると
視点の高さ1mの人の
自分の足元から1m先は何度かという問題。(・・・
「イチイチルート2」とか「イチニイルート3」とかあの辺りを思い出してくれただろうか。
そう、この場合は45°だ。
絵描きとなった今はこれを地面パースに応用する
しかし、まあ当時のように数字にガンと向き合うわけではなく
このような方向性、考え方だということだけを分かってくれれば有難い。
そしてここで求めた角度はメガホンの下視界角と一緒であるということを
頭の隅っこに置いといてくれ。
ちなみにここでの正しい求め方にtan(タンジェント)を用いていたはずだ
視点の高さ
───── = tanθ
足元との距離
さてさて今回はそろそろ終わりに近づいているが
これからどうするのかと先に説明しておくと・・・
絵にとって、視点の高さは定まっているので
この「足元との距離」というのを 1m、2m、3mとして
三角比表というものを用いてそれぞれの角度を調べてみる
そしてそこで求められた角度を前回のあのメモリの付いた絵に使う。
・・・のだが、それでは当初の意と反してまったく実用的ではないので
視点の高さと足元との距離で求められる角度を
1枚の簡単な表に作ってみたので
三角比表ではなく、これを参照に話を進めていくことにしたい。
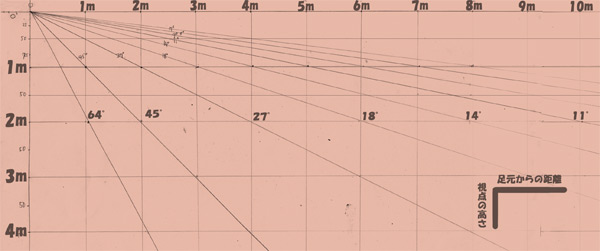
何故飛ばたし。
飛んできた人にもじっくり求め方の方向性を読解された方にもあっけなく分かりやすいように説明したいと思う。
縦が視点の高さ、横が足元からの距離として見てほしい
そうだ。視点の高さ1mの場合、1m先 2m先 3m先などは
下のような角度になっている事が分かるだろうか

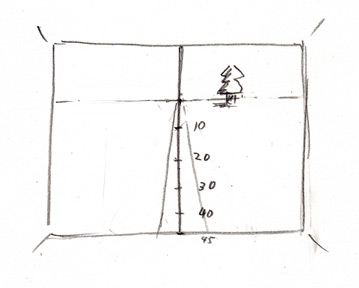
そう、ここで出た角度を前回の角度を付けた絵に使うと
自分から1mごとの線が分かるという
なんともびっくりな優れものになるんだ。
読めるか・・・。
うん、ありがとう
|
|